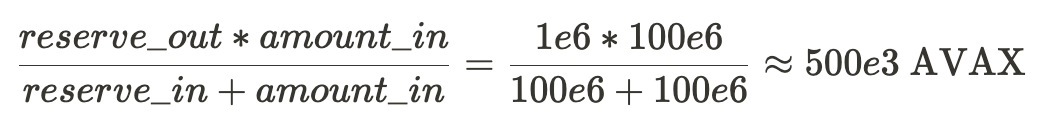This is a 3 part series where we go over 1st generation AMMs, 2nd generation AMMs and finally culminate in our idea of what a modern AMM should look like. Read part 1 here.
Uniswap V2 is the most forked protocol ever. Its simple design meant that any average Joe or Jane could market make. However, its shortcomings — namely impermanent loss, inventory loss and inefficient use of capital — has seen a new generation of AMMs been born. This is a brief overview of them.
Uniswap V3
The main idea behind V3 is concentrated liquidity. This is powerful because your liquidity is being used more efficiently than V2.
Let’s take the USDC/USDT pool as an example.
The price should float around 1 most of the time, so it makes sense to concentrate your liquidity around that price. However, when you provide liquidity on Uniswap V2, you’re providing liquidity evenly over the entire price range (i.e. (0, infinity)).
That means you are providing the same amount of liquidity regardless if the price was 1 or 12345. The chances of price reaching such a high number is so slim that it’s a colossal waste of capital.
Wouldn’t it be better if you take the same amount of liquidity and put it at a range of say, [0.95, 1.05], instead?
Uniswap V3 allows you to do that — liquidity providers get to specify at what range they want to provide liquidity at.
To understand this in more detail, let’s do a quick recap of V2.
Below is the x*y=k graph, where x is the quantity of asset X and y is the quantity of asset Y and price is the slope at any point on the curve (which we define as y/x).
The main takeaway from this graph are the two asymptotes:
As x approaches 0, y approaches infinity
As y approaches 0, x approaches infinity
Put differently, x or y can never be 0.
Therefore, if you provide liquidity to the AVAX/USDC pool then there can never be a scenario where the whole pool is made up of only AVAX or only USDC.
This differs to Uniswap V3, where you can provide liquidity in any range.
Take the graph below.
Trades still adhere to the x*y=k invariant, which is represented by the blue line. However, if someone wants to provide liquidity in price range [a, b], their position is translated to the orange line instead which has formula:
Without getting lost in the details, this formula intercepts both axes and now has possible scenarios for when x or y is 0.
This means that once price exits this range, liquidity composes entirely of a single asset.
For example, Alice provides liquidity in the AVAX/USDC pool at a range of $95-105:
Price below $95: Alice’s LP consists of only AVAX.
Price between $95-105 inclusive: Alice’s LP consists of both AVAX and USDC.
Price above $105: Alice’s LP consists of only USDC.
You may have read how LP’ing on Uniswap V3 is like selling an option on your assets and this is the general idea behind it.
Ok so Uni V3 sounds amazing. Then why are people hating on it?
The main issues are lack of composability and active management of liquidity.
The success of Uni V2 was down to the simplicity of providing liquidity. Every liquidity position in a pool was the same, which meant it could be represented by fungible tokens, which in turn allowed for easy yield farming. It was perfect for the lazy investor.
In Uni V3 however, no two liquidity positions are the same. Therefore, liquidity is represented by non-fungible tokens instead and NFTs just make yield farming hard
To add to that, Uni V3 requires you to constantly readjust the range at which you provide liquidity to make sure price is within it. As a result, it has detracted a lot of retail users from LP’ing.
Pros
Capital efficient
Cons
Lack of composability for yield farming
Requires active management of liquidity
Curve V2
Curve V2 saw Curve venture into the generalised AMM space for the first time. Its new version promises low slippage trades for multiple uncorrelated assets.
At the time of writing, there is only one pool for Curve V2 — the tricrypto pool, which consists of BTC, ETH and USDT.
It works similarly to Curve V1, but instead of targetting $1, it targets the current price as referenced by its internal price oracle which uses an exponential moving average.
The beauty of V2 is that there’s no manual rebalancing required unlike in Uniswap V3. Instead, the pool automatically rebalances liquidity around the oracle price.
For example, let’s say there’s a Curve V2 pool with BTC and USDT, and the current price is $30,000. Most of the liquidity will be concentrated around that price with the rest spread out over a larger price range.
If the price moves to say, $40,000, then the pool will auto-rebalance and liquidity will shift so that $40,000 is the new focal point.
As a result, every liquidity position is the same and can be represented by fungible tokens. Yield farming is back baby!
However, it’s not all sunshine and rainbows. If we look at the empirical data, relative volume is super low compared to the USDC/ETH pool on Uniswap V3:
Tricypto pool:
TVL = $480m
Daily volume = $107m
Vol/TVL = 22%
USDC/ETH 0.05% pool:
TVL = $328m
Daily volume = $693m
Vol/TVL = 211%
Controlled for TVL, the tricrypto pool is doing almost 10x less volume!
My suspicions tell me this is down to a mix of reasons:
Unfriendly user experience
Not properly marketed as a generalised DEX
Inability to to accommodate long tail assets (i.e. bad for shitcoin trading)
Pros:
Fungible liquidity
Capital efficient
Single-asset staking
Cons:
Hard to accommodate for random long tail assets
Time-Weighted Average Market Maker (TWAMM)
First described in this article by Paradigm, the general gist of TWAMMs is to break large orders into small orders over time. Doing so results in better price execution as arbitrageurs step in to bring the price back down after each small order.
This is essentially what whales do. When Michael Saylor decides to buy $100m of Bitcoin, he’ll “TWAP” it by buying in smaller chunks over time.
The graph below illustrates this better:
However, all transactions on the blockchain are public, so even the sub-orders are vulnerable to front-running. For example, say Alice and Bob both want to buy AVAX. If Alice buys before Bob, then Bob will get a worse price as Alice’s buy will bump up the price.
To solve this, buys and sells are grouped together.
How bout sandwich attacks? Technically any public transaction is vulnerable to sandwich attacks, however these are minimised as the TWAMM orders are executed between blocks. This makes it extremely hard to sandwich attack because an attack has to be able to guarantee it will be the last transaction of the first block and the first transaction of the next block in order for the attack to be carried out.
Now consider this situation: AVAX is $100 and there’s 1m AVAX and 100m USDC in the pool. Alice wants to swap 100m USDC and Bob wants to swap 1m AVAX.
Who’s order goes first? We consider the two scenarios:
Alice swaps first:
Alice receives 500k AVAX
Bob receives 133m USDC
Bob swaps first:
Bob receives 50m USDC
Alice receives 1.33m AVAX
Clearly whoever swaps second gets the better deal.
In our example, Bob would like to swap for the exact amount Alice wants to swap out and vice versa. To mitigate this, Bob and Alice just sends theirs tokens to each other and receive a swap with 0% price impact.
Pros:
Allows for bigger trades and replicates traditional finance
Cons:
Still vulnerable to sandwich attacks (but rare)
Increases gas cost
Not really an AMM in itself; more of a layer that can be built on top of other AMMs
Replicating Market Makers (RMM)
A replicating market maker is a market maker whose portfolio matches a target payoff.
That’s a lot of mumbo jumbo so I’ll use Primitive Finance as the example. In Primitive, the fees earned by liquidity providers matches the payoff of a covered call.
Covered Calls
This requires an understanding of options, which I’ll only cover very briefly. A call gives the holder the right but not the obligation to buy an asset at the set price at expiry and a put gives the holder the right but not the obligation to sell an asset at the set price at expiry.
Let’s say AVAX is $100 on 1st June 2022 and Alice buys $110 calls for 1st July 2022 from Bob.
If AVAX rises to $120 on 1st July 2022, Alice can buy AVAX for $110 from Bob and sell it at $120 for instant profit.
If AVAX rises to only $105 on 1st July 2022, then Alice can choose not to exercise her call option and she only loses money from the option premium.
In the tradfi world, options are contracts that are legally enforced. Bob sold the call option to Alice, but he doesn’t have to have the AVAX on hand. In the scenario where AVAX rises to $120, he would end up losing a lot of money because he will have to buy AVAX on the maket at $120 in order to sell it to Alice at $110. This is called a naked call.
In the covered call scenario, Bob would have to have the AVAX on hand prior to selling the call option to Alice. This is equivalent to depositing collateral; since we can’t legally enforce options on the blockchain, all defi call options are covered.
So why would ever want to sell covered calls?
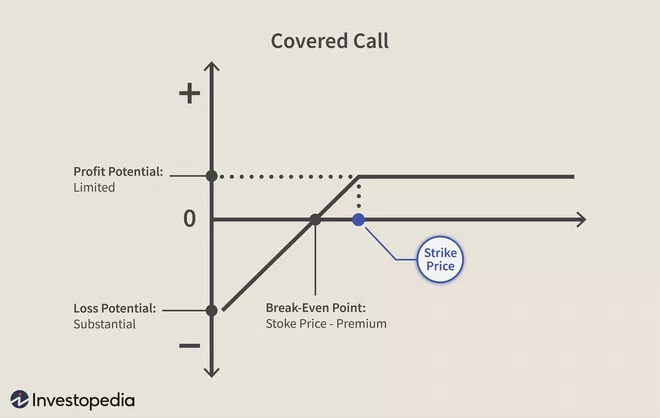
Let’s say AVAX is $100 and Bob is bullish long-term but doesn’t think it will get to $150 by 1st July 2022. He can therefore sell covered calls on his AVAX with a strike price of $150 and so long AVAX is below $150 by 1st July 2022, then he profits from the option premium. In addition, if AVAX has risen to say, $130, he has still profited from the rise in AVAX price as well!
His payoff would look like the chart below; any rise in AVAX price would be profitable for him, until it passes $150, at which point he will lose his AVAX. Thus, the strike price places a cap on his profit potential.
Options Pricing
An option is generally worth more than its payoff up until the moment it expires
Consider the $100 strike AVAX put expiring tomorrow:
If the price of AVAX is currently $100, this put's current payoff is $0
But the price of ETH could fall by tomorrow, in which case the put would be worth more than $0 at expiry
So the put must be worth something greater than $0 now to account for that possibility.
One basic and widely-used model for options pricing is the Black-Scholes model.
It calculates a call/put input price based on:
Strike price
Spot price
Volatility
Expiration
Risk-free rate
The graph below shows the Black-Scholes price of a $3000 strike ETH put compared to the payoff at various spot ETH prices one day before expiry.
So why price options?
Options themselves can be traded
How their price is based on intrinsic value - won’t go into too much detail here
Very rarely do buyers see options out to expiration
Everlasting options - options which never expire / go on in perpetuity
Back to Primitive
Anyways, back to Primitive. We said before that market making here is like writing a covered call option. That means when you supply liquidity, you also have to input parameters like expiry date and strike price like you would for an option:
Essentially, you’re selling a call option on your liquidity, where the option premium are the trading fees accumulated.
When it comes to trading, the main thing to understand about Primitive is it does not use the x * y = k formula. Instead, it uses a formula based on options pricing:
y - KΦ(Φ−1(1 − x) − σ √τ ) = k
This formula produces a curve that’s very similar to x * y = k:
I’m not gonna bother explaining each and every term in this equation, except that τ is the time until expiry. Because this variable is dynamic, it means the curve actually changes over time.
And actually, as time gets closer to expiry, the curve gets flatter and flatter:
If time was the only variable, the curve flattens until trades can be executed at a fixed price equal to the strike price. This is essentially concentrating liquidity like Uniswap V3, but around the strike price.
Let’s say you’ve provided liquidity to the AVAX/USDC pool with strike price of $100 expiring tomorrow. Most of the liquidity is now around $100.
If current price is $90, then arbitrageurs will buy AVAX on other exchanges and sell them on the RMM. Pool will consist of all AVAX.
If current price is $100, then there’s no arbitrage opportunity. Ratio of AVAX and USDC is equal.
If current price is $110, then arbitrageurs will buy AVAX from the RMM and sell it on other exchanges. Pool will consist of all USDC.
Pros:
Also get concentrated liquidity (but over time)
Impermanent loss only occurs if price exceeds the strike price
Allows you to take directional bets on your liquidity
Cons:
Very complicated to add liquidity
Summary
This was a very brief summary of the popular 2nd generation AMMs out there right now. The main ideas of that are improved upon are capital efficiency and better trade execution for large trades. I did skim through it to not make this article mega long, so don’t crucify me.