This is a 3 part series where we go over 1st generation AMMs, 2nd generation AMMs and finally culminate in our idea of what a modern AMM should look like.
First described by Vitalik in this post, Automated Market Makers (AMM) became the catalyst for DeFi. Uniswap is most famous of them all, but there’s more. We cover them in this article.
Uniswap
The basis of Uniswap is the constant product formula, x * y = k, where x is the quantity of asset X, y is the quantity of asset Y and k is a constant. Each pool therefore only comprises of two assets X and Y and this formula ensures the ratio of both are equal.
The chart shows the graph of the constant product formula, where x is the quantity of X and y is the quantity of Y in the pool and the slope to the point on the curve is the spot price.
This is best explained with an example.
Let AVAX be $100 and an AVAX/USDC pool comprise of 20 AVAX and 2000 USDC. Because 20 AVAX is equivalent to 2000 USDC, the ratio of asset values are 1:1. If we let asset X be AVAX and asset Y be USDC, then using the constant product formula we get k = 20 * 2000 = 40000.
This number remains constant during swaps and only changes if more liquidity is added.
Now imagine that Alice wants to swap 5 AVAX. How much USDC will she get in return?
Re-arranging the formula for y, we get y = k/x. So the amount of USDC in the pool after the swap is y = 40000 / (20+5) = 1600 USDC. So Alice received 400 USDC for 5 AVAX.
The pool now comprises of 25 AVAX and 1600 USDC. The spot price of AVAX is now 1600/25 = 64 USDC from 100 USDC (thanks Alice for dumping on all of us).
The price impact of this trade is (64-100) / 100 = -36%.
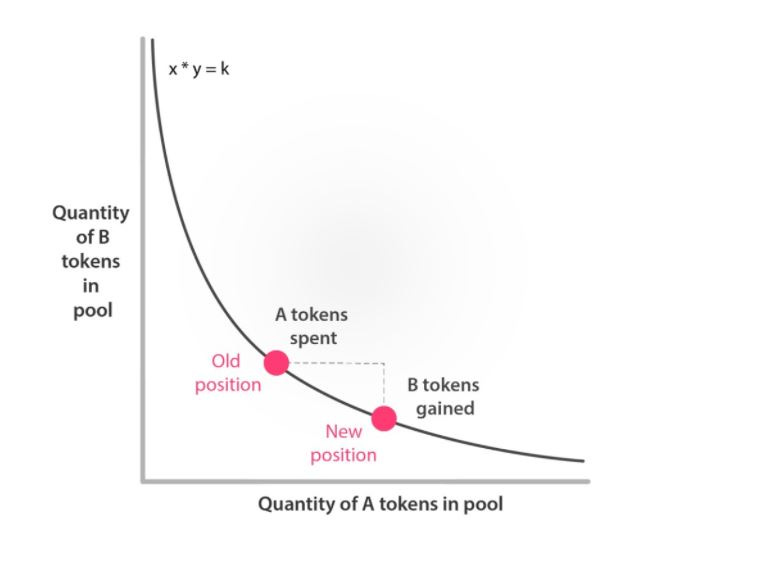
This can be one of the downfalls of constant product market makers - price impact. Because the curve is convex, as you move along the curve the slope constantly changes.
Take the graph below. Imagine a slope at the old position and a slop at the new position. A small change along the curve has produced drastically different slopes, the difference of which is price impact.
The remedy to all this is to make sure liquidity is deep enough to absorb price impact.
However, there’s one massive benefit to this model. If you examine the graph again, you’ll notice that the curve never intercepts the x or y axes. That means there’s never a scenario where the reserves of x or y have been depleted from the pool. By providing in this matter, you can provide liquidity for the entire range of prices (i.e. [0, ∞]) and always have both assets to execute trades.
Such a feature makes liquidity providing extremely easy and basically spurred on the DeFi revolution because now every Joe or Jane can become a market maker, where in the past that job was reserved to big financial institutions.
Balancer
What if we could have each pool consist of more than 2 assets? This is the basis of Balancer, which takes the constant product formula but generalises it for up to 8 assets.
In addition to this, Balancer pools allow for custom ratios. For example, instead of 50:50 in a two asset pool, you can customise it to an 80:20 ratio. There’s a few reasons why you would want to weight an asset more:
You’re more bullish about a certain asset and want it to make up more of your portfolio.
The higher a token’s weight the less impermanent loss it experiences.
This graph depicts how lopsided-pools can reduce IL for the more heavily-weighted token. But this comes at the cost of more price impact for trades within the pool as there’s less liquidity on one side.
Balancer pools can be thought of as automatically rebalancing portfolios that act like decentralised index funds that anyone can create and fees go to liquidity providers instead of intermediary fund managers.
Curve
Uniswap and Balancer both use constant product as the underlying invariant, but one of the downsides is price impact. Enter the constant sum formula. It’s the underlying invariant that powers Curve and solves the issue of high price impact.
The constant sum formula is x + y = k and the graph looks like this:
Remember, price is the slope to the point on the line. In this graph, the slope is always the same; i.e. price is constant, which means zero price impact trades. Sounds brilliant right? There is one caveat. The line intercepts both the x and y axes, which means you will get scenarios where the pool is depleted of one of the assets.
Imagine a constant sum pool for USDC/USDT at $1. If the price of USDC/USDT rises to 1.1 on another exchange, then arbitrageurs will immediately scoop up all the USDC on your pool so they can sell it for profit on the other exchange.
Because of this, Curve uses a modified version of the constant sum formula which is a combination of constant sum and constant product. The actual equation is complicated so I’m going to show you my for dummies version which can be distilled to:
A * (x + y) + xy = k
A is the amplification factor and is dependent on the ratio of reserves. If a pool becomes very unbalanced, A subsequently decreases, minimising the term (x + y). This allows the pool to behave like a constant product market maker.
Conversely, if the pool is very balanced, A is subsequently high which maximises the term (x + y), allowing the pool to behave like a constant sum market maker.
The result is the blue line below, which is flat in the middle as assets equally balanced and convex as the pool becomes heavily in one asset:
Bancor
Bancor launched in 2017 as the very first AMM. It’s main selling point is that it offers 100% impermanent loss protection.
This is a hotly debated topic. No one likes impermanent loss, but is it possible to solve it completely?
As outlined by Hayden Adams in this tweet, you incur more IL by willing to sell close to market price. And since this is the main job of an LP, it’s quite impossible to offer better rates without incurring more IL.

Despite possible solutions on the market, it seems like someone still has to eat the impermanent loss. And the major downside to Bancor’s model is it’s the BNT holders who have to suffer it.
Summary
We cover the protocols that became the bedrock of DeFi. Most use constant product formula except for Curve which uses a modified version of constant sum. The benefits of constant product is liquidity providing made easy, though it does come with the need to have deep liquidity for better price execution.